Dopo aver compreso a cosa servono le resistenze (o resistori) vediamo ora utilizzale all’interno dei nostri schemi elettrici.
Ricapitolando, il calcolo di quale resistenza utilizzare viene fatto mediante la legge di Ohm.
Georg Ohm, un fisico e matematico tedesco, inizio ottocento si accorse di come esista una proporzionalità diretta tra la differenza di potenziale applicata attraverso un conduttore e la corrente elettrica risultante. Questa scoperta avvenne grazie ad un macchinario di sua creazione, di fatto è stato uno dei primi makers della storia.
Prima di iniziare vi ricordo che le resistenze non hanno alcuna direzione, senso o verso. Utilizzarle da sinistra a destra o destra a sinistra produce il medesimo risultato.
Come calcolare quale dev’essere la forza della resistenza da inserire nel circuito è stato già spiegato nel precedente articolo; concentriamoci ora sulle 2 diverse modalità con cui due o più resistenze possono essere collegate al circuito.
Quando non si dispone di una resistenza singola di sufficiente forza (ohm) possiamo ottenere l’effetto desiderato mettendo due o più resistenze in serie o parallelo.
Utilizzando i medesimi resistori optando per la serie o il parallelo otteniamo risultati diversi. E’ molto importante quindi comprenderne le differenze.

Resistenza in serie: si hanno delle resistenze in serie quando l’una viene messa di seguito all’altra. Il circuito elettrico è collegato ad una sola resistenza che a sua volta è collegata e saldata alla seconda resistenza e cosi via. L’uscita verso il sensore o altri elementi del circuito avviene quindi attraverso un solo resistore.
Esiste quindi una ed una sola via che la tensione deve percorrere per passare da
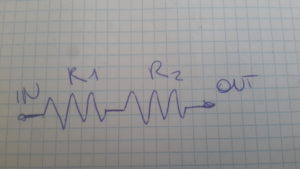
una parte all’altra del circuito elettrico in modo obbligato.
In questo caso, per calcolarne la resistenza totale (Req), si fa la somma del valore di resistenza del primo elemento e del secondo.
Esempio:
Req = R1 + R2 + … Rn
Dove:
Req = resistenza totale
R1..n = Resistore 1, Resistore 2, etc etc…
Ancora un altro esempio pratico con due resistori:
Se abbiamo un resistore da 220 ohm R1 = 220 Ω ed un secondo resistore da 350 ohm R2 = 350Ω collegandoli in serie otterremo una resistenza totale:
(Req) = 220 Ω + 350 Ω = 570 Ω
Resistenza in parallelo: si hanno delle resistenze in parallelo quando i diversi resistori

condividono sia gli ingressi che le uscite del circuito.
A differenza del primo caso dove esisteva una ad una sola via per il passaggio della tensione in questo caso la corrente ha diverse vie pari al numero dei resistori utilizzati.
La tensione elettrica nel caso di resistenza in parallelo risulta la medesima tra i loro estremi.
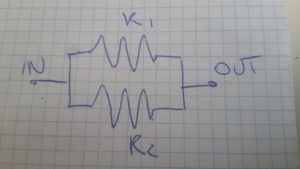
Ecco la formula per calcolare la resistenza totale (Req) se i resistori sono in parallelo: Req = 1/{(1/R1)+(1/R2)+(1/Rn)}
Dove:
Req = resistenza totale
R1..n = Resistore 1, Resistore 2, etc etc…
Quindi, utilizzando i medesimi resistori dell’esempio sopra, collegandoli in parallelo otteniamo:
R1 = 220 Ω
R2 = 350 ohm
Req = 1/{(1/220)+(1/350)} =
= 1/{(0,00454545454545)+(0,00285714285714)} =
= 1/ 0,00740259740259
= 135,0877192983807Ω
Come vedete utilizzando i medesimi resistori otteniamo 2 risultati molto diversi!
Collegati in serie: 570 Ω
Collegati in parallelo: 135 Ω